はじめに
「日本株はアメリカの株価に連動する」
投資をしている人なら一度は聞いたことがある話ではないでしょうか。でも、これって本当なんでしょうか?
私はアルゴリズムトレードのプロジェクトを始めたばかりで、最初の仮説として「日本株価はアメリカに連動する」を検証することにしました。具体的には、S&P500の前日の動きで、日経平均ETFの当日の動きを予測できるかを実際のデータで確認してみました。
この記事では、以下の内容を紹介します:
- 検証した仮説の詳細
- Pythonでの検証方法(コード付き)
- 実際の検証結果(正答率45.89%)
- TOPIXでも検証した結果
- 次のステップ
また、他仮説に関しては次記事を参照ください
検証した仮説「日本株価はアメリカに連動する」
よく聞く話だけど本当?
投資界隈では「日本株はアメリカに連動する」とよく言われます。確かに、ニュースでも「アメリカ株が上がったから日本株も上がった」みたいな解説をよく聞きますよね。
しかし、実際にデータで検証した記事をあまり(少なくとも私は)見かけません。「実際はどうだろう?」という疑問を持ったので、自分で確かめてみることにしました。
具体的に何を検証したのか
今回検証した仮説はこちらです:
仮説:S&P500の前日の動き(上がるor下がる)を使えば、日経平均ETFの当日の動き(上がるor下がる)を予測できる
もう少し具体的に言うと:
- 入力データ:前日にS&P500が上がったか下がったか
- 予測対象:日経平均ETFが当日に上がるか下がるか
- 検証方法:過去データで実際に予測してみて、どのくらい当たるか測定
シンプルですが、「連動するなら予測できるはず」という発想です。
日経平均ETF(1321.T)とは
今回は「日経平均株価そのもの」ではなく、日経平均ETF(ティッカーシンボル:1321.T) を使いました。
ETFは上場投資信託のことで、日経平均ETFは日経平均株価に連動するように設計された金融商品です。個別銘柄ではなく、日経平均全体の動きを反映するため、今回の検証に適していると判断しました。
※ETFについてもっと詳しく知りたい方は、こちらの記事をどうぞ(作成予定)
検証方法と実装
今回の検証は、Pythonのyfinanceライブラリを使って、以下の流れで実装しました:
【実装フロー】
- パラメータ設定
- データ取得(yfinance)
- データ前処理(変動率・方向判定)
- 日付マッチング(米国前日→日本当日)
- データフィルタリング(閾値適用)
- 混同行列作成
- 評価指標計算
それでは、実際のコードとともに見ていきましょう。
Step 1:パラメータ設定とライブラリのインポート
まず、検証条件を設定し、必要なライブラリをインポートします。
【パラメータ設定】
# 検証期間
START_DATE = '2023-01-01' # 検証開始日(YYYY-MM-DD形式)
END_DATE = '2025-10-25' # 検証終了日(YYYY-MM-DD形式)
# 対象銘柄・指数
US_TICKER = '^GSPC' # 米国株(デフォルト: S&P500)
# その他の例: '^DJI'(ダウ平均), '^IXIC'(ナスダック)
JP_TICKER = '1321.T' # 日本株(デフォルト: '1321.T', 日経平均のETF)
# その他の例: '^TOPX'(TOPIX), '1306.T'(TOPIX連動型ETF)
# '7203.T'(トヨタ), '6758.T'(ソニー)
# 米国株の変動閾値(%)
US_THRESHOLD = 1 # この値以上の変動をトリガーとする
# 推奨値: 0.3〜1.0%【ライブラリのインポート】
import yfinance as yf
import pandas as pd
import numpy as np
from sklearn.metrics import confusion_matrixStep 2:データ取得
yfinanceを使って米国株と日本株のデータを取得します。
print("データ取得中...")
# 米国株データ取得(終値のみ)
us_data = yf.download(US_TICKER, start=START_DATE, end=END_DATE, progress=False)
us_df = us_data[['Close']].reset_index()
us_df.columns = ['date', 'us_close']
us_df['date'] = pd.to_datetime(us_df['date'])
print(f"✅ 米国株データ取得完了: {len(us_df)}日分")
print(f" 期間: {us_df['date'].min().date()} 〜 {us_df['date'].max().date()}")
# 日本株データ取得(寄り付きと引けの両方)
jp_data = yf.download(JP_TICKER, start=START_DATE, end=END_DATE, progress=False)
jp_df = jp_data[['Open', 'Close']].reset_index()
jp_df.columns = ['date', 'jp_open', 'jp_close']
jp_df['date'] = pd.to_datetime(jp_df['date'])
print(f"✅ 日本株データ取得完了: {len(jp_df)}日分")
print(f" 期間: {jp_df['date'].min().date()} 〜 {jp_df['date'].max().date()}")
# データの先頭を表示
print("\n米国株データ(最初の5行):")
print(us_df.head())
print("\n日本株データ(最初の5行):")
print(jp_df.head())【出力結果】
【取得したデータ】
左がS&P500のデータ(us_df)、右側が日経平均ETFのデータ(jp_df)
Step 3:データ前処理
変動率の計算と方向判定を行います。
print("データ前処理中...")
# 米国株の変動率計算(前日終値 → 当日終値)
us_df['us_prev_close'] = us_df['us_close'].shift(1)
us_df['us_change_pct'] = ((us_df['us_close'] - us_df['us_prev_close'])
/ us_df['us_prev_close'] * 100)
# 米国株の方向判定(1=上昇, 0=下降)
us_df['us_direction'] = (us_df['us_change_pct'] > 0).astype(int)
# 欠損値を削除(最初の1行は前日がないため)
us_df = us_df.dropna()
print(f"✅ 米国株前処理完了: {len(us_df)}日分")
print(f" 変動率(終値ベース)の範囲: {us_df['us_change_pct'].min():.2f}% 〜 {us_df['us_change_pct'].max():.2f}%")
# 日本株のザラバ変動率計算(当日の寄り付き → 引け)
jp_df['jp_intraday_change_pct'] = ((jp_df['jp_close'] - jp_df['jp_open'])
/ jp_df['jp_open'] * 100)
# 日本株の方向判定(1=上昇, 0=下降)
jp_df['jp_direction'] = (jp_df['jp_intraday_change_pct'] > 0).astype(int)
print(f"✅ 日本株前処理完了: {len(jp_df)}日分")
print(f" ザラバ変動率の範囲: {jp_df['jp_intraday_change_pct'].min():.2f}% 〜 {jp_df['jp_intraday_change_pct'].max():.2f}%")
# 処理後のデータを表示
print("\n米国株データ(処理後、最初の5行):")
print(us_df[['date', 'us_close', 'us_change_pct', 'us_direction']].head())
print("\n日本株データ(処理後、最初の5行):")
print(jp_df[['date', 'jp_open', 'jp_close', 'jp_intraday_change_pct', 'jp_direction']].head())【出力結果】
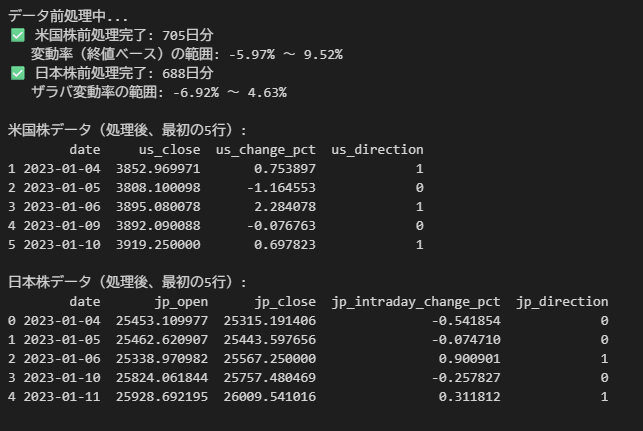
【前処理後のデータ】
Step 4:日付マッチング(米国前日→日本当日)
米国株の「前日」の動きと、日本株の「当日」の動きを紐付けます。
print("日付マッチング中...")
# 米国の日付を1営業日進める(米国前日 → 日本当日)
us_df['date_shifted'] = us_df['date'].shift(-1)
# 最後の行(date_shiftedがNaN)を削除
us_df = us_df.dropna(subset=['date_shifted'])
# 日本市場の日付と結合
merged_df = pd.merge(
us_df[['date', 'date_shifted', 'us_close', 'us_change_pct', 'us_direction']],
jp_df[['date', 'jp_open', 'jp_close', 'jp_intraday_change_pct', 'jp_direction']],
left_on='date_shifted',
right_on='date',
how='inner', # 両方のデータが揃っている日のみ
suffixes=('_us', '_jp')
)
# カラム名を整理
merged_df = merged_df.rename(columns={'date_us': 'us_date', 'date_jp': 'jp_date'})
merged_df = merged_df.drop('date_shifted', axis=1)
print(f"✅ 日付マッチング完了: {len(merged_df)}日分")
print(f" マッチング期間: {merged_df['jp_date'].min().date()} 〜 {merged_df['jp_date'].max().date()}")
# 欠損データの確認
missing = merged_df.isnull().sum()
if missing.sum() > 0:
print("\n⚠️ 欠損データあり:")
print(missing[missing > 0])
else:
print("\n✅ 欠損データなし")
# マッチング結果を表示
print("\nマッチング結果(最初の5行):")
print(merged_df[['us_date', 'jp_date', 'us_change_pct', 'us_direction',
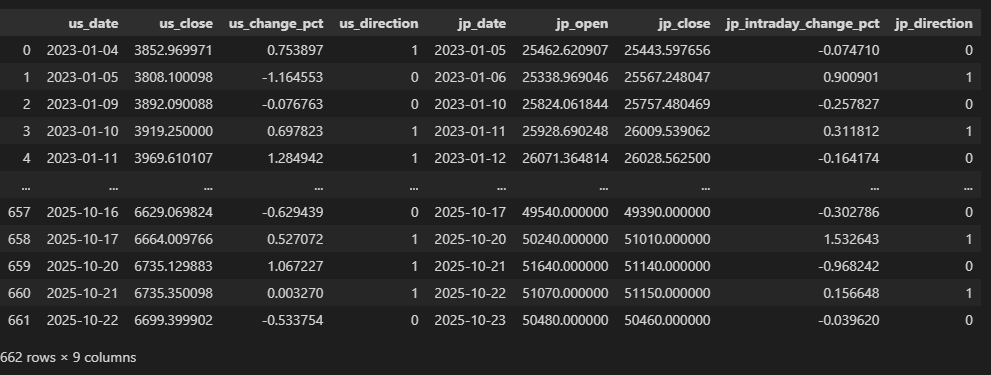
'jp_intraday_change_pct', 'jp_direction']].head())【出力結果】
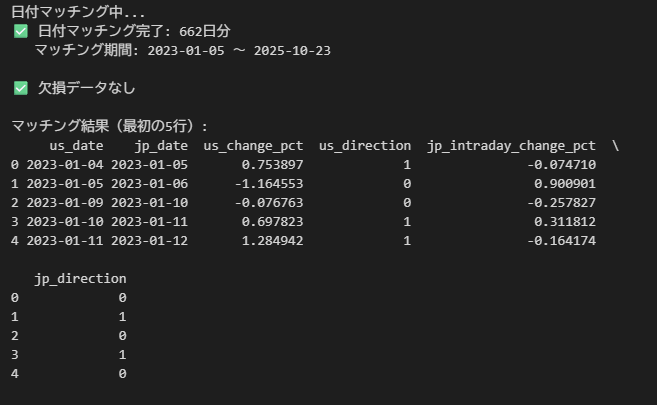
【マージしたデータ】
Step 5:データフィルタリング(閾値適用)
米国株が±1%以上動いた日だけを対象にします。
print("データフィルタリング中...")
# 米国株の変動が閾値以上の日のみを抽出
filtered_df = merged_df[
abs(merged_df['us_change_pct']) >= US_THRESHOLD
].copy()
print(f"\n元データ: {len(merged_df)}日")
print(f"閾値±{US_THRESHOLD}%以上: {len(filtered_df)}日")
print(f"フィルタ率: {len(filtered_df)/len(merged_df)*100:.1f}%")
# フィルタリング後の変動率分布
print(f"\n米国株変動率(終値ベース、フィルタ後):")
print(f" 平均: {filtered_df['us_change_pct'].mean():.2f}%")
print(f" 中央値: {filtered_df['us_change_pct'].median():.2f}%")
print(f" 最大: {filtered_df['us_change_pct'].max():.2f}%")
print(f" 最小: {filtered_df['us_change_pct'].min():.2f}%")
print(f"\n日本株ザラバ変動率(フィルタ後):")
print(f" 平均: {filtered_df['jp_intraday_change_pct'].mean():.2f}%")
print(f" 中央値: {filtered_df['jp_intraday_change_pct'].median():.2f}%")
print(f" 最大: {filtered_df['jp_intraday_change_pct'].max():.2f}%")
print(f" 最小: {filtered_df['jp_intraday_change_pct'].min():.2f}%")
# 方向の分布
us_up = (filtered_df['us_direction'] == 1).sum()
us_down = (filtered_df['us_direction'] == 0).sum()
print(f"\n米国株の方向分布(終値ベース):")
print(f" 上昇: {us_up}日 ({us_up/len(filtered_df)*100:.1f}%)")
print(f" 下降: {us_down}日 ({us_down/len(filtered_df)*100:.1f}%)")
jp_up = (filtered_df['jp_direction'] == 1).sum()
jp_down = (filtered_df['jp_direction'] == 0).sum()
print(f"\n日本株の方向分布(ザラバ):")
print(f" 上昇: {jp_up}日 ({jp_up/len(filtered_df)*100:.1f}%)")
print(f" 下降: {jp_down}日 ({jp_down/len(filtered_df)*100:.1f}%)")【出力結果】

【フィルター後のデータ】
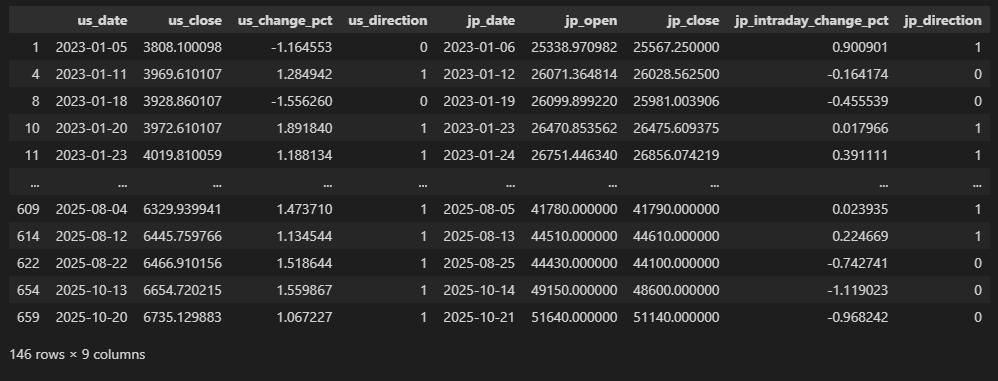
Step 6:混同行列作成
予測(米国の方向)と実際(日本の方向)で混同行列を作成します。
print("混同行列作成中...")
# 予測(米国の方向)と実際(日本の方向)
y_pred = filtered_df['us_direction'] # 予測:米国の方向
y_true = filtered_df['jp_direction'] # 実際:日本の方向
# 混同行列作成
cm = confusion_matrix(y_true, y_pred)
# 混同行列の要素を取得
tn, fp, fn, tp = cm.ravel()
print("\n" + "=" * 60)
print("混同行列")
print("=" * 60)
print(f" 予測:日本↑ 予測:日本↓")
print(f"実際:日本↑ {tp:3d} {fn:3d}")
print(f"実際:日本↓ {fp:3d} {tn:3d}")
print("=" * 60)
print("\n混同行列の意味:")
print(f" TP(真陽性): 米国↑で日本も↑だった = {tp}日")
print(f" TN(真陰性): 米国↓で日本も↓だった = {tn}日")
print(f" FP(偽陽性): 米国↑だが日本は↓だった = {fp}日")
print(f" FN(偽陰性): 米国↓だが日本は↑だった = {fn}日")【実行結果】
Step 7:評価指標計算
正答率、適合率、再現率、F値を計算します。
print("評価指標計算中...")
# 正答率 (Accuracy)
accuracy = (tp + tn) / (tp + tn + fp + fn) if (tp + tn + fp + fn) > 0 else 0
# 適合率 (Precision)
precision = tp / (tp + fp) if (tp + fp) > 0 else 0
# 再現率 (Recall)
recall = tp / (tp + fn) if (tp + fn) > 0 else 0
# F値 (F1-score)
f1_score = (2 * precision * recall / (precision + recall)
if (precision + recall) > 0 else 0)
print("\n" + "=" * 60)
print("評価指標")
print("=" * 60)
print(f"正答率 (Accuracy): {accuracy:.2%}")
print(f"適合率 (Precision): {precision:.2%}")
print(f"再現率 (Recall): {recall:.2%}")
print(f"F値 (F1-score): {f1_score:.2%}")
print("=" * 60)
print("\n評価指標の意味:")
print(f" 正答率: 米国の明確な動きに対し、日本が同じ方向に動いた割合")
print(f" 適合率: 米国↑の日に日本↑と予測した場合の的中率(買いシグナルの信頼性)")
print(f" 再現率: 日本が実際に上昇した日のうち、米国↑で予測できた割合")
print(f" F値: 適合率と再現率のバランス(総合的な予測性能)")【実行結果】
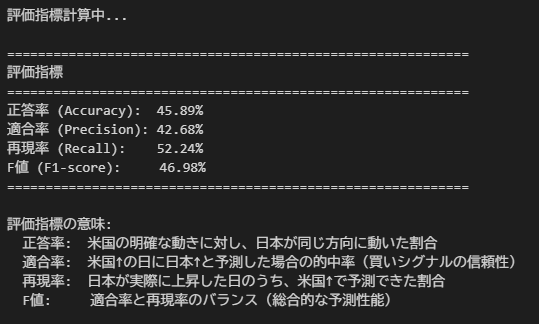
検証結果【正答率45.89%】
この結果が意味すること
一般的に、予測モデルの評価では:
- 50%:ランダム(コイン投げと同じ)
- 45-55%の範囲:ほぼランダム(相関なし)
- 60%以上:ある程度の予測力あり
今回の結果は**45.89%**なので、ランダムとほぼ変わらないと判断できます。
つまり、S&P500の前日の明確な動き(±1%以上)でも、日経平均ETFのザラバを予測できないという結論です。
「日本株はアメリカに連動する」という話は、今回の検証方法では確認できませんでした。
「役立たない」結果も価値がある
「予測できませんでした」という結果は一見失敗に見えますが、これは重要な成果です。
なぜなら:
- リスク回避:使えない手法に時間やお金を使わずに済む
- 次の仮説へ:別のアプローチを試すきっかけになる
- 学び:「なぜ予測できないのか」を考えることで理解が深まる
アルゴリズムトレードでは、こうした「検証して使えないと分かる」プロセスが非常に重要です。
また、パラメータ設定を変更することも可能なので期間や閾値、対象の銘柄を変えることで良い結果になるかもしれません。
日経平均ではなく、TOPIX(1306.T)でも同様にやってみましたが、正答率50%超えませんでした、、、
考察と次のステップ
なぜ連動しなかったのか(仮説)
今回の検証では「連動しない」という結果でしたが、その理由をいくつか考えてみました:
- 時間軸の問題:前日だけでなく、数日前の影響を見る必要があるかも
- ザラバの特性:寄り付き時点で、すでに織り込まれている可能性
- 業種による違い:日経平均全体ではなく、特定の業種(金融、製造業など)や輸出入の多い企業群などで違う結果が出るかも
- 為替や金利の影響:米国株だけでなく、為替レートや金利などの他の要因を考慮する必要があるかも
次に検証すること
今回の結果を受けて、次は以下の検証を進めます:
- 業種別企業での検証:金融、製造業、テクノロジーなど業種ごとに検証
- 関数化してランキング作成:複数の銘柄で一気に検証してランキング化
- 別の仮説の検証:ニュース(決算情報など)の影響を検証
関連記事
- アルゴリズムトレードで検証したい投資仮説5つ → 実装可能な2つ + 新仮説1つに絞り込むまで
- 日経平均・TOPIX・S&P500とは?指数解説(作成予定)
- ETFとは何か解説(作成予定)
- Python環境構築(Google Colab入門)(作成予定)
まとめ

今回は「日本株価はアメリカに連動する」という仮説を検証しました。
結果:S&P500の明確な動き(±1%以上)でも、日経平均ETFのザラバを予測できない(正答率45.89%)
「予測できない」という結果は一見失敗に見えますが、検証して「使えない」と分かったことは重要な成果です。これで無駄なリスクを避けることができます。
次は業種別の検証や、別の仮説(ニュースの影響など)に進んでいきます。アルゴリズムトレードは仮説検証の連続ですが、その過程を楽しみながら続けていきたいと思います!
読者の皆さんも、ぜひ自分で検証してみてください。Pythonとyfinanceがあれば、誰でも簡単に始められますよ。


